Don't believe in the null hypothesis?
Chong Ho (Alex) Yu, Ph.D. (2013)
In a statistical test, the researcher selects between two mutually exclusive hypotheses: the null and the alternate hypothesis. It is a common notion that:
- You don't believe in the null hypothesis
- You do believe in the alternate hypothesis
In this article I explain the logic behind it and why it is not always right.
| The Logic of Falsification |
 The notion of disbelieving in the null hypothesis is based on the principle of falsification introduced by prominent philosopher of science, Karl Popper (1902-1994). According to Popper (1959), we cannot conclusively affirm a hypothesis, but we can conclusively negate it. The validity of knowledge is tied to the probability of falsification. For example, a very broad and general statement such as "Humans should respect and love each other" can never be wrong and thus does not bring us any insightful knowledge. The more specific a statement is, the higher possibility that the statement can be negated. For Popper, a scientific method is "proposing bold hypotheses, and exposing them to the severest criticism, in order to detect where we have erred." (Popper, 1974, p.68) If the hypothesis can stand "the trial of fire," then we can confirm its validity. The notion of disbelieving in the null hypothesis is based on the principle of falsification introduced by prominent philosopher of science, Karl Popper (1902-1994). According to Popper (1959), we cannot conclusively affirm a hypothesis, but we can conclusively negate it. The validity of knowledge is tied to the probability of falsification. For example, a very broad and general statement such as "Humans should respect and love each other" can never be wrong and thus does not bring us any insightful knowledge. The more specific a statement is, the higher possibility that the statement can be negated. For Popper, a scientific method is "proposing bold hypotheses, and exposing them to the severest criticism, in order to detect where we have erred." (Popper, 1974, p.68) If the hypothesis can stand "the trial of fire," then we can confirm its validity.
Today we can still find the influence of Popperian principle of falsification in statistical terminology. For instance, in Structural Equation Modeling (SEM), when the resulting equations fail to specify a
unique solution, the model is said to be untestable or unfalsifiable, because it is capable of perfectly fitting any data i.e. if a model is "always right" and there is no way to disprove it, this model is useless. A good hypothesis or a good model needs a high degree of specification.
Quantification such as the assertion that "the mean of population A is the same as the population B" is considered a high degree of specification. Following the Popperian logic, the mission of a researcher is to falsify a specific statement rather than to prove that it is right. Therefore, the attempt of falsification leads to the disbelief of the null hypothesis.
Many structural equation modelers (SEM will be introduced in another page) subscribe to the Popperian notion because whenever the researcher found a particular "good" model, there are many other equivalent models that could also fit the data. Following this mode of reasoning, McCoach et al. (2007) stated, "In SEM, it is impossible to confirm a model, we can never actually establish its veracity. Statistical tests and descriptive fit indices can never prove that a model is correct" (p.464).
Careful readers may ask, "Why do we distrust and try to falsify the null hypothesis only? Why don't we apply the same action to the alternate hypothesis?" Indeed, current hypothesis testing procedure is a hybrid of schools of Fisher and Neyman/Pearson. Testing the null hypothesis was introduced by R. A. Fisher (1949) while the alternate hypothesis was suggested by Neyman and Pearson (1928).
We can specify the null hypothesis easily, but we don't know what exactly the alternate hypothesis is. We may hypothesize that there is a mean difference between the two populations, but we cannot point out how wide the gap would be. We don't even know from which of the alternate population the test statistic comes from. At most we can say that the difference is not zero.
Indeed, the logic of hypothesis testing is: Given the null hypothesis is true, how likely it is for the
occurrence shown by the data to surface? When the p value is 0.0001, it means that 1 out of 10000 times the data will surface as it did under the assumption of the null.
Because we are confined to start with the null hypothesis only, hypothesis testing is not a fair application of Popperian logic of falsification.
| Cannot "prove" the hypothesis |
Nonetheless, in some sense the Popperian approach to hypothesis testing is still correct: we cannot "prove" the hypothesis. As mentioned previously, the logic of hypothesis testing is: Given the null hypothesis how likely we can observe the data in the long run? It can be expressed as: P(D|H). However, usually what we want to know is: given the data how likely the hypothesis, the model, or the theory is correct? It can be written as: P(H|D). It is important to point out that P(D|H) is not the same as P(H|D). Simply put, "if H then D" does not logically imply "if D then H".
If this seems too complicated, it can be easily illustrated by classic logics. In classic logics there is a type of fallacy called, affirming the consequent, also known as the converse error. For example,
- If the theory is correct, it implies that we could observe Phenomenon X or Data X.
- X is observed.
- Hence, the theory is correct.
The preceding argument sounds reasonable, but consider the following two examples:
- If Thomas Jefferson was assassinated, then Jefferson is dead.
- Jefferson is dead.
- Therefore Jefferson was assassinated.
- If it rains, the ground is wet.
- The ground is wet.
- It must rain.
In both examples, the premise, which is a conditional statement, is right. However, there are more than one explanations that can fit the observation. A person could die of illness. When the floor is wet, the pipe may be leaking; the city workers may be cleaning the streets. Therefore, the conclusion is invalid.
We can apply the same approach to look at a null hypothesis:
- If the treatment is ineffective, it implies that there is no performance gap between the control group and the treatment group.
- Zero difference is observed.
- Hence, the null hypothesis is accepted.
Again, failing to observe a difference could be attributed to other causes. Thus, in hypothesis testing we must state our conclusion as "failing to reject the null hypothesis," but not "accepting the null hypothesis." We have to leave the explanation open to other possibilities.
 At most we can say that we either confirm or disconfirm a hypothesis. There is a subtle difference between "prove" and "confirm." The former is about asserting the "truth" but the latter is noting more than showing the fitness between the data and the model. In philosophy of science this type of fitness is called empirical adequacy. When the data and the model cannot fit each other, again, it is problematic to say that we "prove" the null hypothesis. In the O. J. Simpson case or the Casey Anthony's case, there is not enough evidence to convict the suspect, but it doesn't mean that we have proven the otherwise. By the same token, failing to reject the null hypothesis does not mean that the null is true and thus we should accept it. At most we can say we fail to reject the null hypothesis because the absence of evidence is not the evidence of absence (proving the null). In the article entitled "Absence of evidence is not evidence of absence," Altman and Bland (1995) gave this warning to medical researchers: "Randomized controlled clinical trials that do not show a significant difference between the treatments being compared are often called "negative." This term wrongly implies that the study has shown that there is no difference" (p.485). At most we can say that we either confirm or disconfirm a hypothesis. There is a subtle difference between "prove" and "confirm." The former is about asserting the "truth" but the latter is noting more than showing the fitness between the data and the model. In philosophy of science this type of fitness is called empirical adequacy. When the data and the model cannot fit each other, again, it is problematic to say that we "prove" the null hypothesis. In the O. J. Simpson case or the Casey Anthony's case, there is not enough evidence to convict the suspect, but it doesn't mean that we have proven the otherwise. By the same token, failing to reject the null hypothesis does not mean that the null is true and thus we should accept it. At most we can say we fail to reject the null hypothesis because the absence of evidence is not the evidence of absence (proving the null). In the article entitled "Absence of evidence is not evidence of absence," Altman and Bland (1995) gave this warning to medical researchers: "Randomized controlled clinical trials that do not show a significant difference between the treatments being compared are often called "negative." This term wrongly implies that the study has shown that there is no difference" (p.485).
In reality, we can always find problems with the notion of disbelieving in the null hypothesis. Stevens (1992) gave a good example: Suppose a medical researcher conducts a study to examine the safety of a new drug. His hypotheses would be:
- Null: The new drug has no health benefits
- Alternate: The new drug has health benefits
In this case the doctor should tend to doubt with the alternate hypothesis rather than the null, because if the researcher mistakenly rejects the null and the drug is indeed unsafe, this mistake would cost human lives! In other words, it is a fatal Type I error. There is a real life example in Europe: Once the tranquilizer thalidomide was claimed to be safe but actually the drug was dangerous to pregnant women (cited in Miller & Knapp, 1978).
Nonetheless, McKay Curtis (Personal communication) viewed balancing Type I and Type II errors in drug testing from another perspective:
If a type I error is made and an unsafe drug is approved for use, people could die. This is true. However, Type II errors in this situation could also cost human lives. If a life-saving drug is not approved because of a Type II error, people will also die because they did not have access to the drug. Most people over look this because the consequences of a Type I error are easier to see. It's easier to see that someone has died from a side-effect of an unsafe drug than it is to see that someone has died because he/she didn't have access to a life-saving drug that failed to make it through the statistical hypothesis test. The cost in human lives of a Type II error is just as real as the cost in human lives of a Type I error, even if it is harder to see...The FDA saves lives
by preventing bad drugs from coming to market. But the FDA also costs lives by (sometimes) failing to allow effective drugs come to market. Also, because the FDA has seriously increased the costs (in money and time) of new drug development, drug companies only attempt to develop drugs that are very likely to make it through the approval process.
Some philosophers (e.g. D. H. Lewis) may argue against the preceding notion. In philosophy of causation whether absence of certain events could be counted as a cause has been a controversial topic. Nevertheless, Curtis reminded us that the priority of avoiding Type I or Type II errors is not clear-cut.
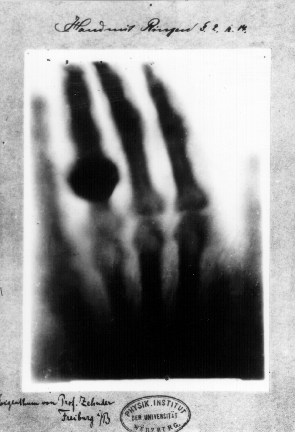 Further,
the discovery of the X-ray was made by "believing" in the null hypothesis
instead of disbelieving in it. In 1895 German physicist Roentgen accidentally
found a fluorescent glow while working with a cathode ray tube. Later he could
see the bone of his hand when this invisible light passed through his flesh. He
was shocked, but instead of immediately announcing it as a scientific
breakthrough to the world, he worked very hard in an attempt to disconfirm what
he found. In other words, the "null" hypothesis is: there is no invisible light
that can pass through human tissues and metals. Nevertheless, he and many other
scientists could successfully replicate the experiment, and thus the alternate
hypothesis was confirmed. The conclusion is more trustworthy because Roentgen
was trying to falsify the finding instead of proving what may look good to his
career (Kean, 2011).
Further,
the discovery of the X-ray was made by "believing" in the null hypothesis
instead of disbelieving in it. In 1895 German physicist Roentgen accidentally
found a fluorescent glow while working with a cathode ray tube. Later he could
see the bone of his hand when this invisible light passed through his flesh. He
was shocked, but instead of immediately announcing it as a scientific
breakthrough to the world, he worked very hard in an attempt to disconfirm what
he found. In other words, the "null" hypothesis is: there is no invisible light
that can pass through human tissues and metals. Nevertheless, he and many other
scientists could successfully replicate the experiment, and thus the alternate
hypothesis was confirmed. The conclusion is more trustworthy because Roentgen
was trying to falsify the finding instead of proving what may look good to his
career (Kean, 2011).
| Balancing Type I and Type II errors |
In most cases the logic of null hypothesis testing follows the
principle of "presumed innocence until proven guilty". However, in public
health it is often trumped by the precautionary principle, which
states that if an action could potentially causing harm to the public or to
the ecology, without scientific consensus, the burden of proof that it is
not harmful is on the shoulder of the party taking the action. In other
words, the precautionary principle prefers "false alarm" (Type I) to "miss"
(Type II).At first glance it makes sense, but the consequence of making a
false alarm could be costly. For example, silicone breast implants have been
commonly available since 1963, and Dow Corning was the major chemical
company that manufactures silicone gel. But after some women who received
the implant complained that they were very ill and the possible cause was
the silicone gel, the US Food and Drug Administration (FDA) conducted a
review and decided there wasn't enough data to show silicone breast implants
were safe. As a precautionary measure, the FDA banned all silicone breast
implants from 1992-2006. It is important to point out that the FDA did not
have evidence to indicate that silicone breast implants are unsafe; rather,
it demanded the evidence to ensure its safety. But the FDA's ban had
triggered a massive flood of lawsuits against Dow Corning. In 1993 Dow
Corning lost more than $287 million. Consequently, Dow Corning was under
Chapter 11 protection from 1993-2004. Nonetheless, later many independent
scientific studies, including the one conducted by U.S. Institute of
Medicine (IOM), found that silicone breast implants do not seem to cause
breast cancers or any fatal diseases. But the company's reputation had
severely damaged, almost beyond redemption (Gardner, 2008).
It is an ongoing debate about the proper use of hypothesis testing. When we use hypothesis testing, we should be aware of the weakness of the logic. Blindly disbelieving the null hypothesis is unwise. Instead, a careful researcher should balance the Type I and Type II error. Neyman and Pearson (1933a), who introduced the concepts of Type I and Type II errors,
recommended that controlling Type II error should be favored in scientific research. Ludbrook and Dudley (1998) argued that in biomedical research it is advisable to control Type I error.
There isn't a clear-cut way for balancing these two errors. The following story illustrates how subjective values would affect the weighing of the hypotheses:
Once a warship is patrolling along the coast. Suddenly an unidentified aircraft appears on the radar screen but the computer system is unable to tell whether it is a friend or a foe.
The captain says:
- The null hypothesis is that the incoming aircraft is not hostile. If it is indeed hostile and I don't fire the missile, it is a Type II error. The consequence of committing this Type II error is that we may be attacked and even killed by the jet.
- The alternate hypothesis is that the incoming aircraft is hostile. But if it is not hostile and I shoot it down, it is a Type I error. The consequence of making this Type I error is the termination of my career in the Navy.
- It seems that the consequence of Type II error is more serious. Therefore, I disbelieve in the null hypothesis. Fire!
The commander shouts "Delay the order!" He argues:
- If the null hypothesis is false but we don't react, the consequence is that a few of us, let's say 30, may be killed.
- If the alternate hypothesis is false and actually the incoming aircraft is a commercial airliner carrying hundreds of civilian passengers, the consequence of committing a Type I error is killing hundreds of innocent people and even starting a war that may eventually cause more deaths.
- I assert that the consequence of Type I error is more severe. Thus, I disbelieve in the alternate hypothesis. Hold the fire!
 The above story is exaggerated to make this point: Subjective values affect balancing of Type I and Type II error and our beliefs on null and alternate hypotheses. A similar scenario could be seen in the movie "Crimson Tide" and two real life examples happened in 1987 and 1988. In 1987 an Iraqi jet aircraft fired missile at the USS Stark and killed 37 US Navy personnel. A patrol plane detected the incoming Iraqi jet and sent the information to the USS Stark, but the Captain did not issue a red alert. A year later the USS Vincennes patrolling at the Strait of Hormuz encountered an identified aircraft. This time the Captain ordered to open fire but later it was found that the US warship shot down an Iranian civilian airliner and killed 290 people. While the former mistake is caused by under-reaction, the latter is due to over-reaction.
The above story is exaggerated to make this point: Subjective values affect balancing of Type I and Type II error and our beliefs on null and alternate hypotheses. A similar scenario could be seen in the movie "Crimson Tide" and two real life examples happened in 1987 and 1988. In 1987 an Iraqi jet aircraft fired missile at the USS Stark and killed 37 US Navy personnel. A patrol plane detected the incoming Iraqi jet and sent the information to the USS Stark, but the Captain did not issue a red alert. A year later the USS Vincennes patrolling at the Strait of Hormuz encountered an identified aircraft. This time the Captain ordered to open fire but later it was found that the US warship shot down an Iranian civilian airliner and killed 290 people. While the former mistake is caused by under-reaction, the latter is due to over-reaction.
The founders of hypothesis testing, Neyman and Pearson (1933b) asserted that there is no general rule for balancing errors; in any given case, the determination of "how the balance [between Type I and Type II errors] should be struck, must be left to the investigator." On the contrary, Lipsey (1990) gave a specific guideline: In basic research it is desirable to keep the probability of Type I error low. It is because the nature of basic research is that the researcher should be very conservative about accepting new facts or changing facts of existing knowledge. On the other hand, in applied research it is preferable to minimize the Type II error rate because in a situation where effective treatment is needed and not readily available, a Type II error can represent a great practical loss.
On the other hand, Wang (1993) asserted that the Type I and Type II errors as well as the accept-reject method are useful only for certain engineers in quality control when clear rules of decision are needed. But in general science one can use confidence interval to solve most problems without the help from the analysis of Type I or Type II errors.
In summary, balancing Type I and Type II errors has "nothing to do with statistical theory, but are based instead on context-dependent pragmatic considerations where informed personal judgment plays a vital role" (Hubbard & Bayrri, 2003, p.173).
Altman, D., & Bland, M. (1995). Statistics notes: Absence of evidence is not evidence of absence. BioMedical Journal, 311, 485.
Fisher, R. A. (1949). The design of experiments. London: Oliver and Boyd.
Gardner, D. (2008). The science of fear: Why we fear the things we
shouldn't--and put ourselves in greater danger. New York, NY: Dutton Adult.
Hubbard, R., & Bayarri, M. J. (2003). Confusion over measures of evidence (p's) versus errors (alpha's) in classical statistical testing. American Statistician, 57, 171-178.
Kean, S. (2011). The disappearing spoon: And other true tales of madness,
love, and the history of the world from the periodic table of the elements.
New York, NY: Back Bay Books.
Lipsey, M. W. (1990). Design sensitivity: Statistical power for experimental research. Newbury Park: Sage Publication.
Ludbrook, J. & Dudley, H. (1998). Why permutation tests are superior to t and F tests in biomedical research. American Statistician, 52, 127-133.
McCoach, D. B., Back, A. C., & O'Connell, A. A. (2007). Errors of inference in structural equation modeling. Psychology in the Schools, 44, 461-470.
Miller, J. K. & Knapp, T. R. (1978). The importance of statistical power in educational research. (ERIC Document Reproduction Service No. : ED 152 838).
Neyman, J. & Pearson, E. S. (1928). On the use and interpretation of certain test criteria for purposes of statistical inference. Part I and II. Biometrika, 20, 174-240, 263-294.
Neyman, J. & Pearson, E. S. (1933a). The testing of statistical hypotheses in relation to probabilities a priori. Proceedings of Cambridge Philosophical Society, 20, 492-510.
Neyman, J. & Pearson, E. S. (1933b). On the problem of the most efficient tests of statistical hypotheses. Philosophical Transactions of Royal Society;, Series A, 231, 289-337.
Popper, K. R. (1959). Logic of scientific discovery. London : Hutchinson.
Popper, K. R. (1974). Replies to my critics. In P. A. Schilpp (Eds.), The philosophy of
Karl Popper (pp.963-1197). La Salle: Open Court.
Stevens, J. (1992). Applied multivariate statistics for the social sciences. Hillsdale, NJ: Lawrence Erlbaum Associates, Publishers.
Wang, C. (1993). Sense and nonsense of statistical inference: Controversy, misuse, and subtlety. New York: Marcel Dekker, Inc.
Navigation
Index
Simplified Navigation
Table of Contents
Search Engine
Contact
|
 The notion of disbelieving in the null hypothesis is based on the principle of falsification introduced by prominent philosopher of science, Karl Popper (1902-1994). According to Popper (1959), we cannot conclusively affirm a hypothesis, but we can conclusively negate it. The validity of knowledge is tied to the probability of falsification. For example, a very broad and general statement such as "Humans should respect and love each other" can never be wrong and thus does not bring us any insightful knowledge. The more specific a statement is, the higher possibility that the statement can be negated. For Popper, a scientific method is "proposing bold hypotheses, and exposing them to the severest criticism, in order to detect where we have erred." (Popper, 1974, p.68) If the hypothesis can stand "the trial of fire," then we can confirm its validity.
The notion of disbelieving in the null hypothesis is based on the principle of falsification introduced by prominent philosopher of science, Karl Popper (1902-1994). According to Popper (1959), we cannot conclusively affirm a hypothesis, but we can conclusively negate it. The validity of knowledge is tied to the probability of falsification. For example, a very broad and general statement such as "Humans should respect and love each other" can never be wrong and thus does not bring us any insightful knowledge. The more specific a statement is, the higher possibility that the statement can be negated. For Popper, a scientific method is "proposing bold hypotheses, and exposing them to the severest criticism, in order to detect where we have erred." (Popper, 1974, p.68) If the hypothesis can stand "the trial of fire," then we can confirm its validity. At most we can say that we either confirm or disconfirm a hypothesis. There is a subtle difference between "prove" and "confirm." The former is about asserting the "truth" but the latter is noting more than showing the fitness between the data and the model. In philosophy of science this type of fitness is called empirical adequacy. When the data and the model cannot fit each other, again, it is problematic to say that we "prove" the null hypothesis. In the O. J. Simpson case or the Casey Anthony's case, there is not enough evidence to convict the suspect, but it doesn't mean that we have proven the otherwise. By the same token, failing to reject the null hypothesis does not mean that the null is true and thus we should accept it. At most we can say we fail to reject the null hypothesis because the absence of evidence is not the evidence of absence (proving the null). In the article entitled "Absence of evidence is not evidence of absence," Altman and Bland (1995) gave this warning to medical researchers: "Randomized controlled clinical trials that do not show a significant difference between the treatments being compared are often called "negative." This term wrongly implies that the study has shown that there is no difference" (p.485).
At most we can say that we either confirm or disconfirm a hypothesis. There is a subtle difference between "prove" and "confirm." The former is about asserting the "truth" but the latter is noting more than showing the fitness between the data and the model. In philosophy of science this type of fitness is called empirical adequacy. When the data and the model cannot fit each other, again, it is problematic to say that we "prove" the null hypothesis. In the O. J. Simpson case or the Casey Anthony's case, there is not enough evidence to convict the suspect, but it doesn't mean that we have proven the otherwise. By the same token, failing to reject the null hypothesis does not mean that the null is true and thus we should accept it. At most we can say we fail to reject the null hypothesis because the absence of evidence is not the evidence of absence (proving the null). In the article entitled "Absence of evidence is not evidence of absence," Altman and Bland (1995) gave this warning to medical researchers: "Randomized controlled clinical trials that do not show a significant difference between the treatments being compared are often called "negative." This term wrongly implies that the study has shown that there is no difference" (p.485).
 Further,
the discovery of the X-ray was made by "believing" in the null hypothesis
instead of disbelieving in it. In 1895 German physicist Roentgen accidentally
found a fluorescent glow while working with a cathode ray tube. Later he could
see the bone of his hand when this invisible light passed through his flesh. He
was shocked, but instead of immediately announcing it as a scientific
breakthrough to the world, he worked very hard in an attempt to disconfirm what
he found. In other words, the "null" hypothesis is: there is no invisible light
that can pass through human tissues and metals. Nevertheless, he and many other
scientists could successfully replicate the experiment, and thus the alternate
hypothesis was confirmed. The conclusion is more trustworthy because Roentgen
was trying to falsify the finding instead of proving what may look good to his
career (Kean, 2011).
Further,
the discovery of the X-ray was made by "believing" in the null hypothesis
instead of disbelieving in it. In 1895 German physicist Roentgen accidentally
found a fluorescent glow while working with a cathode ray tube. Later he could
see the bone of his hand when this invisible light passed through his flesh. He
was shocked, but instead of immediately announcing it as a scientific
breakthrough to the world, he worked very hard in an attempt to disconfirm what
he found. In other words, the "null" hypothesis is: there is no invisible light
that can pass through human tissues and metals. Nevertheless, he and many other
scientists could successfully replicate the experiment, and thus the alternate
hypothesis was confirmed. The conclusion is more trustworthy because Roentgen
was trying to falsify the finding instead of proving what may look good to his
career (Kean, 2011). The above story is exaggerated to make this point: Subjective values affect balancing of Type I and Type II error and our beliefs on null and alternate hypotheses. A similar scenario could be seen in the movie "Crimson Tide" and two real life examples happened in 1987 and 1988. In 1987 an Iraqi jet aircraft fired missile at the USS Stark and killed 37 US Navy personnel. A patrol plane detected the incoming Iraqi jet and sent the information to the USS Stark, but the Captain did not issue a red alert. A year later the USS Vincennes patrolling at the Strait of Hormuz encountered an identified aircraft. This time the Captain ordered to open fire but later it was found that the US warship shot down an Iranian civilian airliner and killed 290 people. While the former mistake is caused by under-reaction, the latter is due to over-reaction.
The above story is exaggerated to make this point: Subjective values affect balancing of Type I and Type II error and our beliefs on null and alternate hypotheses. A similar scenario could be seen in the movie "Crimson Tide" and two real life examples happened in 1987 and 1988. In 1987 an Iraqi jet aircraft fired missile at the USS Stark and killed 37 US Navy personnel. A patrol plane detected the incoming Iraqi jet and sent the information to the USS Stark, but the Captain did not issue a red alert. A year later the USS Vincennes patrolling at the Strait of Hormuz encountered an identified aircraft. This time the Captain ordered to open fire but later it was found that the US warship shot down an Iranian civilian airliner and killed 290 people. While the former mistake is caused by under-reaction, the latter is due to over-reaction.