Mathematical Reality:
An Inquiry into the Existence of Theoretical Distributions
and its Implication for Psychological Researchers

Abstract

Modern science are said to be anti-platonic but yet Fisherian theoretical distributions are pervasively used in statistical inferences. The purpose of this article is to determine the existence of theoretical distributions subsumed within mathematical reality, and highlight several meaningful implications for psychological researchers to consider in the application of statistical procedures. Therefore, we begin with a brief overview of the misinterpretation of statistical testing, followed by a discussion of mathematical reality. In addition, ideas for and against theories of mathematical reality by noted scholars are presented, and inconsistencies within these theories are elucidated. Finally, the conclusion highlights practical implications for researchers when implementing statistical procedures.

Introduction

In statistics, we apply theoretical distributions to determine the significance of a test statistic. However, Sir R. A. Fisher, the founder of statistical hypothesis testing, asserted that theoretical distributions against which observed effects are tested have no objective reality "being exclusively products of the statistician's imagination through the hypothesis which he has decided to test." (Fisher, 1956, p.81). In other words, he did not view distributions as outcomes of empirical replications that might actually be conducted. In a similar fashion, Lord (1980) "delinked" the statistical world and the real world:

A statistician doing an Analysis of Variance does not try to define the model parameters as if they existed in the real world. A statistical model is chosen, expressed in mathematical terms undefined in the real world. The question of whether the real world corresponds to the model is a separate question to be answered as best we can. (p.6)

Mathematicians have developed a world of distributions and theorems. Essentially, statistical testing is a comparison between the observed statistic and theoretical distributions to decide which hypothesis should be retained, based upon the central limit theorem. The conclusion obtained is then reported as the results of a particular study. This in itself is not problematic to the advancement of basic and applied research; in fact it is central to it. However, many psychological researchers employ statistics without questioning its underlying philosophy. This becomes problematic when the results are interpreted as the empirical truth based upon an empirical methodology while indeed the methodology is not empirical-based. Therefore, an awareness of how statistical testing found its base in the scientific method is imperative.

Questions regarding the basis of statistical testing lead directly to its philosophical foundations. To be specific, how could we justify collecting empirical observations and using a non-empirical reference to make an inference? Are the t-, F-, Chi-square, and many other distributions just from a convention imposed by authorities, or do they exist independently from the human world, like divine moral codes? Whether such distributions are human convention or divine codes, the basis of distributions remains the same: distributions are theoretical in nature, and are not yet proven.

Nevertheless, empirical reality is one of many forms of realities (Drozdek & Keagy, 1994). Reality, by definition, is an objective existence which is independent from human perception (Devitt, 1991). Alternatively, mathematical reality is proposed as a foundation to justify mathematical-based methodologies such as statistical testing.

It is important to note that this article focuses on theorems and distributions rather than certain "cut-off" decisions, which are defined and determined by human intuition and convention. For instance, in regard to statistical significance, there is a well-known saying that "God loves the .06 nearly as much as the .05." for debunking the myth of alpha level (Rosnow & Rosethal, 1989; Cohen, 1990). One and a half of the inter-quartile range (IRQ) as the criterion for classifying outliers and non-outliers is another good example. When Paul Velleman asked John Tukey, the father of exploratory data analysis who invented the boxplot and the 1.5*IQR Rule, "Why 1.5?', Tukey replied, "Because 1 is too small and 2 is too large." (Cook, 1999). By the same token, the classification of low, medium, and high effect size and power are also arbitrary conventions. Issues of this kind does not fall into the philosophical discussion of ultimate reality.

Although this article focuses on ultimate reality, it does not attempt to determine the existence of all ultimate realities. Statistics is a subset of mathematics. The question whether statistical theorems and distributions are real is essentially subsumed by the broader question of mathematical reality. Further, the question of mathematical reality is tied to general ontological reality. An investigation of the latter is beyond the scope of this paper. This article concentrates on mathematical reality, which has been thoroughly discussed in philosophy.

Mathematical realism, which assumed that mathematical entities exist independently of human cognition, dates back to the era of Plato ¹. Thus, mathematical realism is often associated with Platonism. It was popular in the late 19^th century. However, it lost popularity in the 20^th century with the emergence of non-Euclidean geometries and set theory. Instead, formalism became the dominant force. Those who adhere to formalism view mathematical formulas as just formulas, a set of rules for convenience. In fact, this view is shared by statisticians who believe statistical modeling is nothing more than a convenient way for description and prediction; the model is not intrinsic to the phenomenon itself (Tirri, 2000). Nonetheless, support for mathematical realism has been revived recently (Drozdek & Keagy, 1994). The purpose of this article is to determine the existence of theoretical distributions subsumed within mathematical reality, and highlight several meaningful and practical implications important to researchers in the application of statistical testing. In so doing, the following section will give a brief account of ideas for and against theories of mathematical reality noted by major scholars. The discussion will focus on the inconsistencies within these theories, followed by a conclusion of practical benefit to researchers. It is important to note that the problem of mathematical reality and the controversy of hypothesis testing will not be solved in this article.

Discussion of mathematical reality pertaining to statistics is very rare. Most mathematicians and philosophers center discussions on geometry, algebra, and other branches of mathematics. Therefore, philosophy of mathematics seems to be remote and even irrelevant to social science researchers. Although the following review of major theories of mathematical reality is not directly based on statistics, their implications are still important to the applications of theoretical distributions.

Platonic Worlds

Most philosophers relate mathematical realism to Platonism ² (Tieszen, 1995). For Plato, epistemology and ontology are almost inseparable. Plato asserted that beyond this physical sphere there is a metaphysical world (reality): "Form." Mathematical concepts (knowledge) exist in that timeless, eternal and ideal world. In the physical sphere we see substances, which are the realization of the ideal forms in the metaphysical world. He illustrated this point by the following metaphor: We are tied inside a cave and are forced to look at one direction only. Someone uses fire as the projection light and manipulates objects behind our back. When we see the projection on the wall, we perceive the shadow as the reality without knowing there is another dimension of reality (Copleston, 1985).

Following Plato's analogy, normal distributions never exist in this world because they are just the projection of a perfectly normal distribution from the ideal world. Geary (1947) observed deviations from normality and asserted that "Normality is a myth; there never was, and never will be, a normal distribution." (p.241). This assertion may be a stumbling block to researchers who apply statistical methodologies. To Platonists, normality is a reality and there is a perfectly normal distribution behind the projection. In short, the ultimate reality exists beyond the human cognitive and physical reality. Therefore, one may intuit that mathematical reality, including statistical theorems and distributions, is a valid existence in the Platonic framework.

Wittgenstein's Approach

Intuitionistic Approach

Wittgenstein was strongly opposed to the preceding Platonic notion. His view of mathematics is termed "intuitionistic approach," the definition of which is that human knowledge could vary from time to time and from place to place, according to human intuition. He regarded human knowledge, including both philosophy and mathematics, as the product of language. In his view, mathematical theories are the description of observed or experienced phenomena constructed by humans. When the knowledge of mathematics is viewed as semantic and linguistic, mathematics may not involve ontology, thereby the question of mathematical reality is unnecessary.

Saying and Showing

Further, he asserted that numbers cannot be regarded as elements in the same sense as words. Sentences can be explained in "telling" but mathematical equations must be expressed by "showing." For example, to prove "two plus two equals four " one can show two oranges first and two oranges later. The classification of "numbers" and "words" leads to his rejection of the Law of Excluded Middle, in which we select between two known options such as "true" or "false." He questioned whether every mathematical statement possess a definite sense that there must be something in virtue of which either it is true or it is false. In Wittgenstein's view, the question we should ask is not whether a statement or a proposition is true or false. Instead, the problem is whether it makes sense to us under certain circumstances (Wittgenstein, 1922; Gonzalez, 1991).

Although the existence of and mathematical reality has no room in Wittgenstein's framework, his classification of telling and showing can be applied to advance our knowledge of theoretical distributions. More details of the application will be given in the discussion section.

Russell's Approach

Russell (1919) disagreed with intuitionistic approach and affirmed the existence of unchanged structures in mathematics. In philosophy of science, his leading motive is to establish certainty in an attempt to replace the Christian faith he rejected. Russell found certainty in mathematics, because he believed that mathematical objects are eternal and timeless (Hersh, 1997). In Russell's view, in order to uncover the underlying structures of these eternal objects, mathematics should be reduced to a more basic element, namely, logic. Thus, his approach is termed logical atomism.

Russell's philosophy of mathematics is mainly concerned with geometry rather than statistics (1919). Nonetheless, the question of knowing the existence of geometric objects resembles the question of knowing the existence of theoretical distributions. At the time of Russell, the existence of geometric objects and the epistemology of geometry cannot be answered by empiricists. In geometry a line can be broken down infinitely to a smaller line. We cannot see or feel a mathematical line and a mathematical point. Thus, it is impossible that geometric objects are objects of empirical perception (sense experience). Then how could conceptions of such objects and their properties be derived from experience as an empiricist would require if geometry is to be allowed to have any application to the world of experience? Russell's answer is that although geometric objects are theoretical objects, we can still understand geometric structures by applying logic to study relationships among those objects. "What matters in mathematics, and to a very great extent in physical science, is not the intrinsic nature of our terms, but the logical nature of their inter-relations." (p.59).

Whitehead and Russell (1950) asserted that even if the whole human race becomes extinct, symbolic logic would persist. In their book Principia mathematica, they devoted tremendous efforts in an attempt to develop a fully self-sufficient and proved mathematical entity. However, this bold plan is seriously challenged by Kurt Godel, who proposed that a complete and consistent mathematical system is inherently impossible.

Godel's Theorem

Kurt Godel, the great mathematician who was strongly influenced by phenomenology, took an "intuitionistic" position. His famous Godel's theorem is a counterattack against Whitehead and Russell's notion. Phenomenology is a school of philosophy introduced by Husserl, which maintains that reality is the result of perceptual acts and we should "bracket" phenomena whereas their essences are unknown to us. Godel asserted that it is not a question whether there are some real objects "out there," rather, our sequences of acts construct our perceptions of so-called "reality." According to Godel, "Despite their remoteness from sense experience, we do have something like a perception also of the objects of set theory, as is seen from the fact that the axioms force themselves upon us as being true. I don’t see any reason why we should have any less confidence in this kind of perception, i.e. in mathematical intuition, than in sense perception." (cited in Lindstrom, 2000, p.123)

In Godel's theorem, a system is either complete or consistent (Chaitin, 1998). Thus, logically speaking, it is impossible for us to fully "prove" any proposition. In our experience we intuit objects as complete and whole but indeed only parts of an object are reachable to us. If there is no mathematical entity, inferences based upon mathematics would be regarded as a leap of faith (Tieszen, 1992).

The assertion by Einstein that nothing can exceed the speed of light imposes a limitation on space travel. By the same token, the notion by Godel that no mathematical system can be proved fully may render the answer to the question, "Do theoretical distributions exist?" insurmountable.

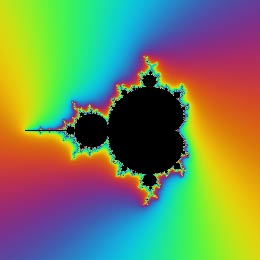
Mandelbrot Set

Several modern mathematicians, such as Mandelbrot, attempted to revitalize the Platonic notion. With the help of high-powered computer, Mandelbrot (1986), who introduced the Mandelbrot fractal set, found that repeated computations lead to the approximation of the same fundamental mathematical structure. It made no difference which computer was used for performing calculations. Fractal sets appear to be random but there are unifying rules to govern the appearance of each beautiful fractal. Therefore, he asserted that the Mandelbrot set, as well as other mathematical theorems, are not mere inventions of the human mind, rather they exist independently. The Mandelbrot fractal set is used by physicists as an example to support the notion that order is embedded in chaos. This notion is known as the chaos theory. The implication of chaos theory goes beyond the existence of mathematical reality to the existence of a general ontological reality, which serves as the foundation of all knowledge. In Mandelbrot's framework, the existence of theoretical distributions can be implied when results of simulations approximate these distributions. The slide show on the right shows examples of fractal set created in Adobe Photoshop with KPT fractal Explorer.

God's Revelation

Oxford mathematician Penrose (1989) looked at the internal structure of math rather than its empirical aspect. After reviewing the Cauchy integral formula, the Riemann mapping theorem and the Lewy extension property, Penrose asserted that the beauty and structure of mathematics are given by God. Mathematicians do not invent equations and formulas. Rather they discover the wonderful creations of the supreme being. Further, Penrose asserted that Plato's world of mathematical concepts is a warrant of communications between mathematicians. Since each mathematician can make contact with Plato's world directly, they can share a common frame of reference (Lindstrom, 2000). This theory, then, supports the existence of mathematical reality, and therefore theoretical distributions, as given by God.

The World is Round

The preceding argument made by Penrose resembles what Socrates raised thousands of years ago. Socrates endorsed the idea that knowledge is grounded on generally agreed definitions (so-called "What is F?" question) and a common frame of reference rather than an individual's perception. If knowledge is just perception, then no one can be wiser than any one; one can be his own judge and any dialog between people is impossible (Copleston, 1984). In defending mathematical realism, Drozdek and Keagy (1994) made a similar assertion:

Realism keeps mathematicians on guard much more than the intuitionist approach would do. For a realist, there is this objective sphere which is an ultimate yardstick of a theory's validity. For an intuitionist, the intuition is the ultimate guide, and if distorted, or turned from well established logical principles, it has nothing, even in theory, to found this statement. (p.340)

Charles Sanders Peirce also emphasized the communicability among scholars. Peirce believed that inquiry is a self-correcting process by the intellectual community in the long run (Yu, 2006). If the intuitionist approach is adopted, the advancement of statistics, psychology, and other disciplines may be hindered.

Discussion

According to Plato, Russell, Mandelbrot, and Penrose, mathematical reality does exist, which implies the existence of theoretical distributions. However, equally learned scholars such as Wittgenstein and Godel do not believe the existence of mathematical reality can be proved. Which scholar should be believed? Each theory is important to the debate of the existence of mathematical reality and theoretical distributions; each theory embodies valid and invalid assertions. Beginning with Russell and Whitehead, the discussion will focus on the inconsistencies within each theory. Following the discussion, the conclusion will highlight several practical implications for researchers to consider when implementing statistical procedures.

Human Gives Meanings to Statistics

Unlike Penrose, Russell rejected the idea of God, but claimed certainty of eternal mathematical objects. Penrose's position is understandable, but Russell's rejection of a metaphysical or supernatural reality and embracing the eternal existence of mathematical objects at the same time is not harmonious. Modern astronomists pointed out that this material universe cannot last forever. New star systems are born as supernovas and old star systems collapse into black holes. Given that the material universe is not eternal, how is it that "eternal mathematical objects" exist when there is no metaphysical or supernatural universe?

Further, Russell's assertion is a problem rather than an answer. In theory, sampling distributions is composed of infinite cases. The problem is that no one can live eternally to see these distributions. Based on the notion of eternal existence, Russell asserted that without humans, mathematical logic still persists This is not logically conceivable because first no one can wipe out the entire human race to test this notion (unless one takes control of nuclear arms), and second, with no human left who can see and feel mathematical objects?

Indeed, mathematics would not be meaningful without the presence of humans, the giver of meanings. Without the existence of human beings, concepts such as "love," "justice," "morality," "freedom" do not make sense. What are freedom and slavery if there are no humans on this planet to become oppressor, oppressed, and free people? Could a rock oppress a tree? Could a mountain be a free being? Once some dolphins rescued a drowning swimmer by pushing her back to the store. A scientist said that those dolphins didn't care about human lives. Rather they just acted out of their instinct and therefore there was nothing noble about their action. By the same token, when animals kill other animals for food, we cannot accuse them as "cold blood murders." Again, they just act out of their impulse. In short, value-laden concepts, including moral concepts and statistical concepts, must be interpreted within the human community. Therefore, one may question the validity of Russell¹s assertion that the reality of mathematical and logical structure does indeed exist.

Change and unchanged

In keeping with this skepticism, Wittgenstein favored relative knowledge over absolute truths. In his view, reality is based upon knowledge, which is in a continuous state of change. Thus, reality is unknown, including mathematical reality. However, it is important to note that change is built upon the unchanged. For example, one may have perceived that "X = A," and then changed perceptions to regard "X as B." Does this change imply that "truth" is fleeting? Not exactly. Before we can say that X has changed, we must have the concepts that "once X was A" and "now X is B." An analogy may be taken from the movie industry: A film clip can be seen as animation because the clip is composed of still frames. It would be naive to deny the existence of static frames just because we see the full animation of the motion picture. As Drozdek and Keagy (1984) points out, the intuitionistic approach hinders the academic circle from dialog and further advancement of knowledge.

Telling and Showing

Black (1959) criticized that nowhere in his writings did Wittgenstein explain how knowledge could be conveyed by "showing." However, Wittgenstein's theory can facilitate the investigation of mathematical reality through the distinction between "showing concepts" on mathematical form and "telling concepts" in linguistic form. Using "the best fit" in statistics as an example, when a regression model is shown as a curve passing as many points as possible with the least square, it is undeniable that it's the best fit. It is important to note that in Wittgenstein's theory, "showing" does not confirm or disconfirm things. As mentioned before, it just shows what makes sense rather than to assert what is true or false. Nevertheless, if knowledge such as "two plus two equals four" and "the best fit" can be shown, can the existence of theoretical distributions be implied, if not proved, by showing? Computer simulation is a modern way of "showing" mathematical knowledge.

Exist in Theory and Exist in Simulations

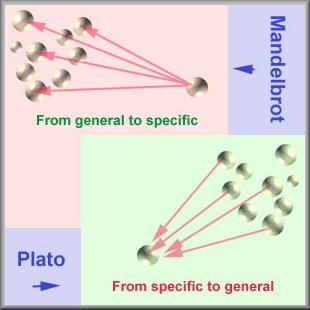Mandelbrot's approach is the opposite of the Platonic approach. Plato starts from particulars in the physical world. Because of the imperfection and chaos in particulars, he extracted the properties of particulars and deduced the existence of a perfect and universal reality. His method can be viewed as a "bottom-up" approach. Mandelbrot works in a reverse manner. He starts from generic mathematical equations and produces a variety of specific fractals. This can be regarded as a "top-down" approach. This simulation approach rectifies the weakness of Platonic speculation.

With the advancement of high-powered computers, simulation is often employed by mathematicians and statisticians as a research methodology. This school is termed as "experimental mathematics," as opposed to "pure mathematics." Chaitin (1998) is one of the supporters of experimental mathematics. He asserted that it is a mistake to regard a mathematical axiom as a self-evident truth. Rather the behaviors of numbers should be verified by computer-based experiments.

If sampling distributions that we use for hypothesis testing exist in theory, do they really exist? Following Mandelbrot's approach, someone may argue that distributions at least exist in simulations. No doubt results based upon computer simulations are more convincing than "pure theories." However, a new question emerges: If something exists in simulations, does it have an authentic existence?

"The borg has assimilated all theoretical distributions!"

In a Star Trek episode entitled The Big Good Bye, the computer-simulated characters in the holodeck asked Captain Picard whether they would vanish when humans leave the holodeck, Captain Picard could not give a definite answer. I have the same puzzle as Picard's. In theory, a sampling distribution is based on infinite cases, but in actuality no one could run a simulation forever. With the use of supercomputers, we might be more confident to claim that empirically speaking a particular theorem is likely to be true. However, comparing with infinity, a simulation with billions of cases is like a drop in the ocean!

Conclusion

We cannot answer whether theoretical distributions exist or not. However, statistical procedures are being applied in psychological research every day, and therefore a firm understanding of their rationale and appropriate application are of the utmost importance. There are three implications to social scientists pertaining to the discussion of theoretical distributions:

1. Because of the inconclusive nature of mathematical reality and theoretical distributions, researchers should not regard the outcome of hypothesis testing as a firm and true answer built upon empirical substantiation. Indeed, the foundation of statistics is theoretical rather than empirical. There is a common belief that in parametric tests an inference is made from the sample (empirical observation) to the population (unobserved). This practice is known as "inverse inference." (Seidenfeld, 1979) Actually, the opposite is true! In hypothesis testing, the nature of the inference is "direct inference." The inference is made to the sample based on a pre-determined sampling distribution. The direction of the inference is more like from the unobserved to the empirical rather than from the empirical to the unobserved.

2. In spite of the uncertainty in the foundation of statistics, researchers in social sciences must start from somewhere even though the starting point is not empirically based. In fact, even physical scientists have to work with many unknowns and uncertainties (Chaitin, 1998). In the first half of the 20th century, verificationism derived from positivism dominated the scientific community. For a while statistics is associated with positivism. For positivists unverified beliefs should be rejected. Nevertheless, according to Peirce, researchers must start from somewhere, even though the starting point is an unproven assumption. This approach is very different from positivism and opens more opportunities for inquirers (Callaway, 1999). In the Peircean framework, theoretical distributions as a starting point are acceptable. However, it is not suggesting that researchers can blindly put their faith on statistics. Rather, researchers should monitor the progress of experimental mathematics and Monte Carlo simulations so that we can apply the best available methodology.

3. Researchers should examine whether their philosophical belief is compatible with the methodology they employ. Hersh (1997) observed an interesting phenomenon: Platonism was and is believed by many mathematicians. However, in the twentieth-century certain scientific communities became anti-metaphysic. Platonism is like an underground religion. It is observed in private but rarely mentioned in public. This inconsistency could be found among psychologists. In public metaphysical assumptions are not discussed. Although in practice theoretical distributions and statistical tests are employed without referring to the question of mathematical reality, a hidden "ontological commitment" is made. When one operates a VCR or tests a nuclear device, one makes an ontological commitment to physical realism (Hersch, 1997). By the same token, when a psychological researcher utilizes theoretical distributions, he makes an ontological commitment to mathematical reality. It is hoped that this article can raise the awareness of this problem and encourage psychologists to confront the inconsistency.

   If researchers do not want to build their research on theoretical distributions, there are other alternatives such as resampling and exploratory data analysis. In resampling, inferences are derived from an empirical distribution (Edgington, 1995; Good, 1994). Researchers do not need to contemplate the philosophical problem of theoretical distributions. In exploratory data analysis, no pre-determined hypothesis needs to be tested and thus probabilistic inferences may not be necessary (Cleveland, 1993). In the spirit of exploratory data analysis, Diaconis (1985) also examined the applicability of probability-free theories. For this reason, Tukey (1986) carefully differentiate ¡§data analysis¡¨ and ¡§statistics.¡¨ While statistics is related to probability theory, data analysis may use probability where it is needed and avoid it when we should. It is hoped that this article can help psychological researchers choosing the research methodology that is compatible with his/her philosophical view.

1. Pythagora is said to be the first thinker to propose the theory that the ultimate essence of everything in the world is number. It is a common practice to call any thinker who see the natural world as ordered according to pleasing mathematical principles a Pythagorean. However, whether this idea should be attributed to Pythagoras is questionable. (Burket, 1972; Heath, 1981). On the other hand, Plato's philosophy is well-documented (Hersh, 1997). Therefore, this article starts the discussion from Plato rather than from Pythagora.

2. The equivalence between mathematical realism and Platonism can be misleading. Realism does not neccesarily presuppose a Platonic epistemology. There are realists who believe that some mathematical objects are not eternal and do enter into causal relationships with material objects (Maddy, 1992).

Black, M. (1959). The nature of mathematics: A critical survey. Peterson, NJ: Litlefield, Adams & Co.

Burket, W. (1972). Lore and science in ancient Pythogoreanism. Cambridge, MA.

Callaway, H. G. (1999). Intelligence, Community, and Cartesian Doubt. [On-line] Available URL: http://www.door.net/arisbe/menu/library/aboutcsp/callaway/intell.htm

Chaitin, G. J. (1998). The limits of mathematics: A course on information theory and the limits of formal reasoning. Singapore: Springer-Verlag.

Cleveland, W. S. (1993). Visualizing data. Summit, NJ: Hobart Press.

Cohen, J. (1990). Things I have learned (so far). American Psychologist, 45, 1304-1312.

Cook, P. (1999). Introduction to exploring data: Normal distribution. [On-line] Available URL: http://curriculum.qed.qld.gov.au/kla/eda/normdist.htm.

Copleston, F. (1984). A history of philosophy: Book one. New Yoek: Image.

Devitt, M. (1991). Realism and truth. (2nd ed.). Cambridge, MA: B. Blackwell.

Diaconis, P. (1985). Theories of data analysis: From magical thinking through classical statistics. In D. C. Hoaglin, F. Mosteller, & J. W. Tukey. (Eds.). Explorating data tables, trends, and shapes (pp. 1-36). New York: John Wiley & Sons.

Drozdek, A. & Keagy, T. (1994). A case for realism in mathematics. Monist, 77, 329-344.

Edgington, E. S. (1995). Randomization tests. New York : M. Dekker.

Fisher, R. A. (1956). Statistical methods and scientific inference. Edinburgh: Oliver and Boyd.

Geary, R. C. (1947). Testing for normality. Biometrika, 34, 209-241.

Gonzalez, W. J. (1991). Intuitionistic Mathematics and Wittgenstein. History and Philosophy of Logic, 12, 167-183.

Good, P. I. (1994). Permutation tests : a practical guide to resampling methods for testing hypotheses. New York: Springer-Verlag.

Heath, Sir T. L. (1981). A history of Greek mathematics. New York: Dover.

Hersh, R. (1997). What is Mathermatics, really? Oxford: Oxford University Press.

Lindstrom, P. (2000). Quasi-realism in mathematics. Monist, 83, 122-149.

Lord, F. (1980). Applications of item response theory to practical testing problems. Hillsdale, NJ: Lawrence Erlbaum Associates.

Maddy, P. (1992). Realism in mathematics. Oxford, UK: Oxford Univbersity Press.

Mandelbrot, B. B. (1986). Fractals and the rebirth of iteration theory. In H. O. Peitgen & P. H. Richter (Eds.), The beauty of fractals: Images of complex dynamical systems (pp.151-160). Berlin: Springer-Verlag.

Penrose, R. (1989). The emperor's new mind: Concerning computers, minds, and the laws of physics. Oxford: Oxford University Press.

Rosnow, R., & Rosenthal, R. (1989). Statistical procedures and the justification of knowledge in psychological science. American Psychologist, 44, 1276-1284.

Russell, B. (1919). Introduction to mathematical philosophy. London: Allen & Unwin.

Seidenfeld, T. (1979). Philosophical problems of statistical inference: Learning from R. A. Fisher. London, England: D. Reidel Publishing Company.

Tieszen, R. (1992). Kurt Godel and phenomenology. Philosophy of Science, 59, 176-194.

Tieszen, R. (1995). Mathematical realism and Godel's incompleteness theorem. In P. Cortois (Eds.), The many problems of realism (pp.217-246). The Netherlands: Tiburg University Press..

Tukey, J. (1986). The collected works of John W. Tukey (Volumn IV): Philosophy and principles of data analysis: 1965-1986. Monteery, CA: Wadsworth & Brooks/Cole.

Whitehead, A. N., & Russell, B. (1950). Principia mathematica (2nd ed.). Cambridge, UK: Cambridge University Press.

Wittgenstein, L. (1922). Tractatus logico-philosophicus. London, UK: Kegan Paul.

Yu, C. H. (2006). Philosophical foundations of quantitative research methodology. Lanham, MD: University Press of America.